March 25, 2003
Exchange Rates

Purchasing Power Parity
Suppose hockey sticks sell for $12 Canadian in Canada and $10 U.S. in the U.S. If the exchange rate is $2/3 U.S. to $1 Can (or $1.50 Can to $1 U.S.), then there is a profit to made buying hockey sticks in Canada and selling them in the U.S. market.
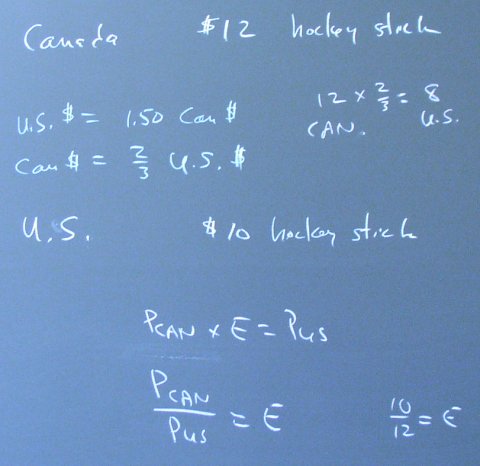
This profit goes away if the Canadian price increases to $15, the U.S. price decreases to $8, or the exchange rate changes to 10/12. Which number will change?
There is considerable intellectual appeal to this theory, but the empirical support for PPP is not at all clear. You will see phrases like "the Mexican peso is overvalued" in the paper. This means that somebody thinks that the peso will go down in value eventually to the level implied by PPP. In reality, trade flows are large and countries run surpluses or deficits over long periods of time, suggesting that PPP takes a long time to move the exchange rate if it ever does.
Interest Rate Parity
If the Canadian interest rate is 8% and the U.S. interest rate is 5%, investors in either country will prefer Canadian bonds. Canadian bonds are considered comparable in risk to U.S. bonds in the N.Y. financial markets, which are closer to Canada then they are to North Carolina.
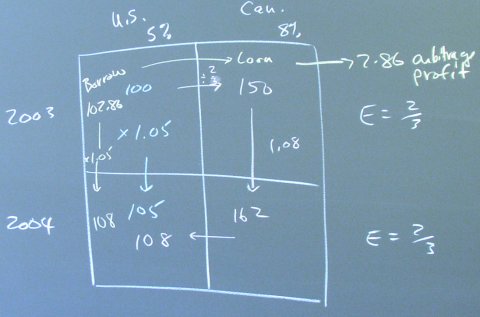
Investors can secure an arbitrage profit by borrowing $102.86 in the U.S. financial markets and loaning out $100 U.S. in the Canadian financial markets, putting a $2.86 U.S. arbitrage profit in their pockets immediately. Note that the futures market for the Canadian dollar allows them to lock in the exchange rate for 2004.
We can express the equation that must hold to shut off these arbitrage profits as:
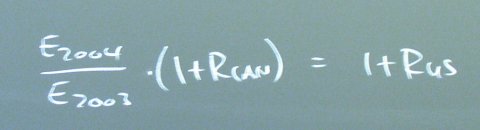
Which number changes to achieve interest rate parity? That is a good question that could take up many lectures. What we can see is that, if the U.S. interest rate is fixed by U.S. monetary policy, then the Canadian central bank can choose to set its exchange rate or its interest rate, but is going to have problems trying to set both numbers.
Posted by bparke at March 25, 2003 11:12 AM